Номинальная стоимость денег не всегда может соответствовать фактической. Ключевое понятие здесь — стоимость денег во времени (СДВ). Вычисления, выполняемые над денежными суммами, могут производиться в прошлом, настоящем или в будущем времени. Выбор типа вычислений основывается на том, что сумма денег увеличивается, поскольку постоянно поступают начисления по процентам. Другими словами, вложив один рубль сегодня, завтра вы получите больше.
Например, предположим, что богатенький заокеанский дядюшка решил подарить вам деньги, причем вы должны выбрать один из перечисленных ниже вариантов.
- Получить 800 000 руб, сегодня,
- Получить 950 000 руб. через год.
- Получить 1 200 000 руб. через пять лет.
- Получать 15 000 руб. каждый месяц на протяжении пяти лет.
Чтобы получить максимальную выгоду, нужно учитывать не только собственно номинальную сумму, но и ту стоимость, которую будут представлять деньги на момент, когда вы их получите на руки.
Стоимость денег во времени зависит от ваших возможностей и перспектив. Другими словами, вы можете быть либо кредитором, либо заемщиком. Когда вы берете кредит на покупку автомобиля, вы выступаете в роли заемщика, а учреждение, которое дает вам деньги, — в роли кредитора. Когда же вы вкладываете деньги в банк на депозит (сберегательный счёт), вы — кредитор, поскольку занимаете свои деньги банку, а банк является вашим заемщиком.
Со стоимостью денег во времени связано еще несколько понятий:
• Приведенная (текущая) стоимость. Это основная сумма, или капитал, на который начисляются проценты. Например, если на депозит в банке вкладывается 500 000 руб., то эта величина представляет собой капитал или приведенную (текущую) стоимость вложенных денег. Если берется ссуда 1 размером 1 500 000 руб. на приобретение автомобиля, то данная сумма будет основной или приведенной стоимостью ссуды. Приведенная стоимость | может быть как положительной, так и отрицательной.
• Будущая стоимость. Представляет собой сумму приведенной (текущей) стоимости и начисленным по ней процентам. Например, если на депозитный счет в банке вкладывается 50 000 руб. на пять лет под 6% годовых, то в конце; срока можно будет получить 66 911,28 руб. Последняя сумма будет будущей стоимостью инвестиции. Если же берется ссуда на три года на покупку автомобиля в размере 150 000 руб. под 7% годовых, то в конце срока нужно будет выплатить 240 867,22 руб. Иными словами, нужно будет вернуть основную сумму плюс проценты. Будущая стоимость, в зависимости от перспектив (кредитор или заемщик), может быть положительной или отрицательной.
• Взнос. Взносом (платежом) может быть либо капитал, либо капитал и начисленные на него проценты. Если каждый месяц вкладывается по 1 000 руб. на депозитный счет, то 1 000 руб. — это взнос. Если для погашения ccyды ежемесячный взнос составляет 8 250 руб., то он состоит из тела кредита (основной суммы) и начисленных процентов.
• Процентная ставка. Часть основной суммы (в процентах), начисляемая определенный период (как правило, за год). Например, деньги могут быть вложены в банк на депозит с процентной ставкой 5,5% годовых. Или процентная ставка по кредиту может составлять 7,75% в год.
• Период. Промежуток времени, по истечении которого выплачиваются проценты (например, банк может выплачивать проценты по депозитам ежеквартально, тогда как кредит за купленный автомобиль чаще всего приходится гасить ежемесячно).
• Срок. Промежуток времени, на который вкладываются или берутся в кредит деньги. Например, деньги вкладываются в банк на депозит на срок один год, или ссуда берется на срок 30 лет.
Финансовые функции
Аргументы функций для финансовых расчетов
- Ставка — процентная ставка за один период. Если она выражена в процентах за год, то эту величину нужно разделить на количество периодов (обычно месяцев).
- Кпер — общее количество выплат (периодов).
- Период — заданный период, который должен быть меньше или равен значению параметра Кпер.
- Пс — приведенная стоимость, или основная сумма.
- Плт — сумма, которая вносится за каждый период (постоянная величина).
- Бс — необязательный аргумент, равный будущей стоимости после последней выплаты. Если аргумент опущен, то он полагается равным нулю. (Например, будущая стоимость ссуды после ее погашения, очевидно, равна нулю.)
- Тип -указывает, когда должны производиться платежи. Равен нулю, если платежи выполняются в конце периода, и единице — если в начале. Это необязательный аргумент, который по умолчанию равен нулю.
1. Функция ПЛТ
Функция ПЛТ позволяет рассчитать размер выплат по кредиту (основная сумма плюс проценты) за один период, полагая постоянными размер выплат и процентную ставку. Эта функция имеет такой синтаксис: ПЛТ (Ставка; Кпер; Пс; Бс; Тип).
2. Функция ОСПЛТ
Функция ОСПЛТ возвращает основную часть платежа по кредиту за определенный период, подразумевая постоянным размер выплат и фиксированную процентную ставку. Функция имеет следующий синтаксис: ОСПЛТ (Ставка; Период; Кпер; Яс; Бс; Тип)
3. Функция ПРПЛТ
Функция ПРПЛТ вычисляет ту часть общей суммы выплат по кредиту, которая идет на погашение процентов, полагая постоянными размер выплат и процентную ставку. Функция имеет следующий синтаксис: ПРПЛТ (Ставка; Период; Кпер; Пс; Бс; Тип)
Найдите размер оплаты, а также основную и процентную сумму для любого периода, задаваемого параметром в ячейке B9, для нижеприведённой ссуды.
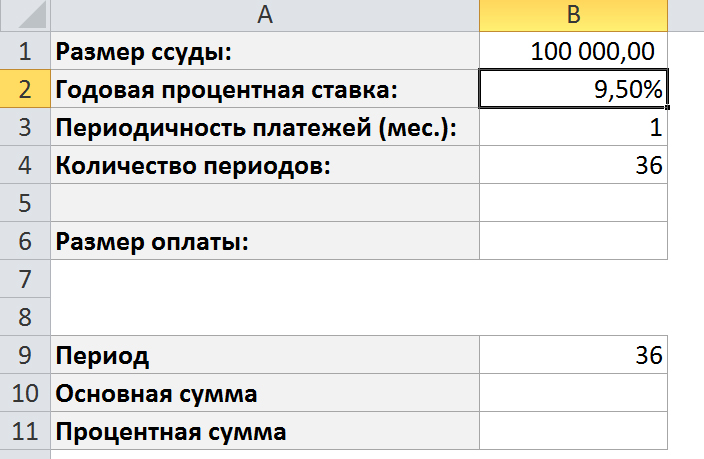
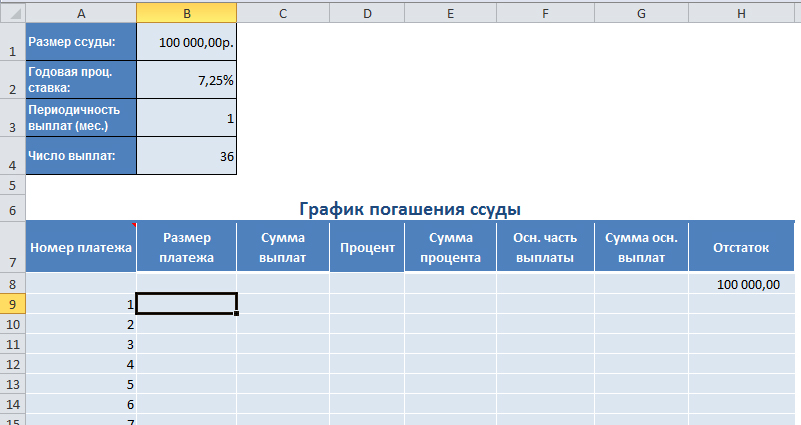
Создайте график погашения ссуда для всех 36 периодов.
- Размер платежа находит функция ПЛТ.
- Сумма выплат создаётся накопительным итогом размером платежа, то есть в ячейке B9 должно быть B8+A9.
- Процент находится с помощью функции ПРПЛТ, причём обращаем внимание на правильное использование абсолютных и относительных ссылок.
- Сумма процента определяется как процент накопительным итогом.
- Основная часть выплаты находится с помощью функции ОСПЛТ.
- Сумма основной части выплат определяется как основная часть выплат накопительным итогом.
- Остаток определяется как накопительная разность основной частью выплат от размера ссуды (пс), то есть H8-F9.
4. Функция БС (будущая стоимость)
Вычисление простого процента
В случае простого процента сумма выплаченных процентов не прибавляются к основной сумме вклада. Чтобы вычислить доход на основании простого процента, используется приведенная ниже формула.
Доход = Основная_Сумма * Процентная_Ставка * Срок
Например, предположим, что в банк на депозит вложено 10 000 руб. на один год, при условии, что простая годовая процентная ставка составляет 5%. Через год банк вернет сумму вклада, а также выплатит проценты в размере 500 руб. Итого сумма выплаты составит 10 500 руб. В этом случае, чтобы вычислить полученные проценты, следует умножить основную сумму (10 000 руб.) на процентную ставку (0,05) и на срок 1 год.
Вычисление сложного процента
В большинстве случаев выплаты по процентам вычисляются на основе одного из типов сложного процента. Под сложным процентом понимается многократное начисление процентов, которые добавляются к общей сумме вклада, причем в следующий раз проценты начисляются как по основной сумме вклада, так и по начисленным ранее процентам.
Например, предположим, что сумма депозита в банке составляет 10 000 руб. Годовая процентная ставка составляет 5%, проценты начисляются каждый месяц. После первого месяца проценты начисляются по основной сумме вклада, а затем полученная сумма выплат по процентам добавляется к основной. В следующем месяце проценты будут начисляться уже по большей сумме (основная плюс выплаты по процентам за первый месяц). Полученная сумма снова добавляется к текущей сумме вклада. Чтобы вычислить объем инвестиции в конце срока, можно создать последовательность формул.
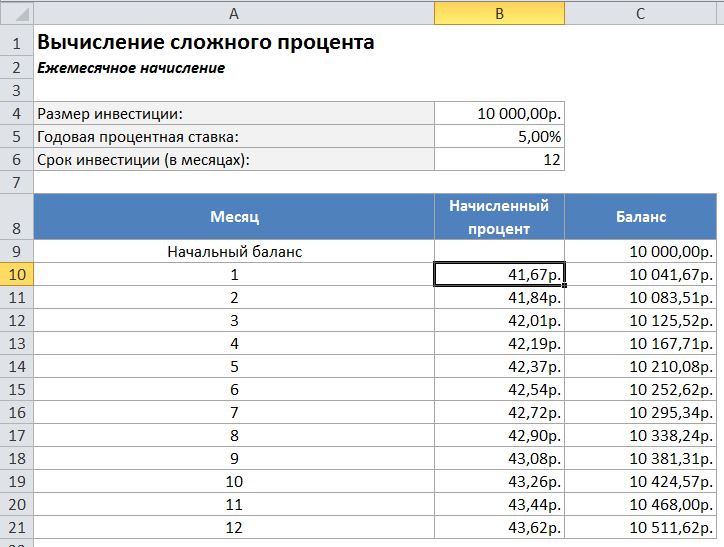
Но такой сложный процент можно посчитать в одной ячейке с помощью функции БС.
Решите следующую задачу с помощью функции БС самостоятельно:
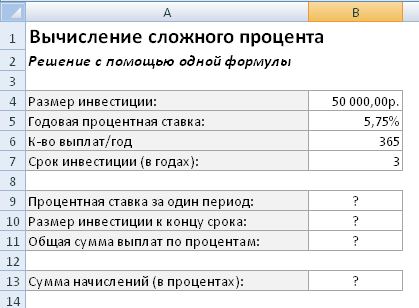
Расчёт аннуитета
Рассмотрим еще один тип инвестиций, в котором на протяжении всего срока инвестиции следует периодически делать дополнительные вклады. Этот тип инвестиции называется аннуитетом. Некоторые банковские учреждения предлагают такую услугу.
Функции, описанные в предыдущих упражнениях, также можно применить и для расчета аннуитетов. Через заданный промежуток времени определенная сумма вносится на депозит. Затем, например через один год, выплачивается вся накопленная сумма (вместе с начислениями по процентам).
Предположим, что в начале каждого месяца (на протяжении 12 месяцев) на счет вносится 2000 руб. под 4,25% годовых, начисляемых ежемесячно. Следующая формула позволяет вычислить будущую стоимость депозита:
= БС(0,0425/12; 12; -2000; ;1)
Формула вернет значение 24 559,74 руб. Это число представляет собой сумму общего объема взносов (24 ООО руб.) и начислений по процентам (559,74 руб.). Последний аргумент функции БС равен 1, это значит, что взносы производятся в начале каждого периода (по умолчанию 0, что значит в конце периода).
Решите задачу расчёта аннуитета при следующих параметрах.
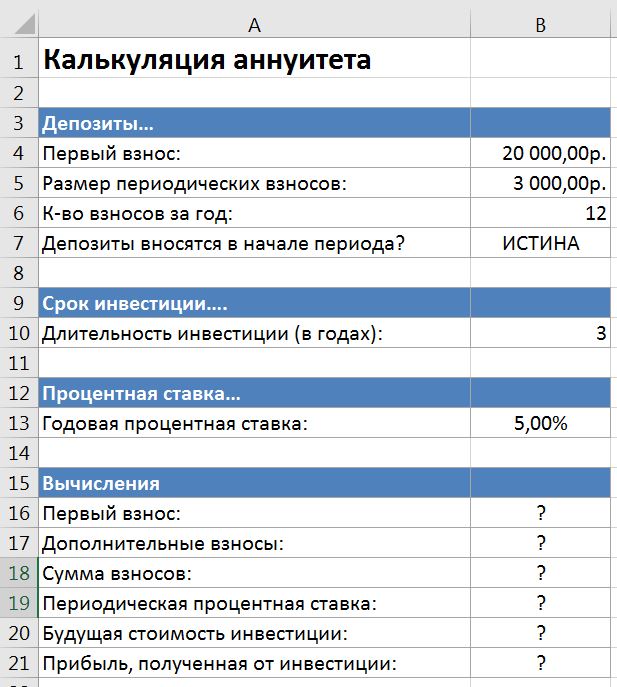
Первый взнос и равен первому взносу (он же и является приведённой суммой), а дополнительные взносы определяются как все периодические взносы (которые в функции БС будут аргументом плт) за все периоды. Сумма взносов – сумма первого взноса и дополнительных взносов. Периодическая ставка – ставка за период. Будущую стоимость инвестиции определяем с помощью функции БС. А прибыль = разнице будущей стоимости и суммы взносов.





