 Перспектива. Это слово заставляет кровь каждого, кто стремится стать художником (и даже многих художников, кто, казалось бы, весьма хороши в том, что делают) стынуть в жилах. Этот «метод рисования 3D-форм в двумерном пространстве» полон запутанных математических правил, которые, как может показаться, не имеют ничего общего с беззаботным и в то же время наполненным страстью рисованием. Даже если вам удалось понять эти правила, возможно, вам до сих пор интересно, как же они применяются к реальному миру. Когда вы смотрите вокруг, вы видите перспективу с одной или двумя точками схода? Если горизонт всегда на уровне глаз, что случится, если вы посмотрите вниз? Что такое точка схода на самом деле? И можно ли вам забыть о перспективе, если вы не рисуете что-то связанное с архитектурой?
Перспектива. Это слово заставляет кровь каждого, кто стремится стать художником (и даже многих художников, кто, казалось бы, весьма хороши в том, что делают) стынуть в жилах. Этот «метод рисования 3D-форм в двумерном пространстве» полон запутанных математических правил, которые, как может показаться, не имеют ничего общего с беззаботным и в то же время наполненным страстью рисованием. Даже если вам удалось понять эти правила, возможно, вам до сих пор интересно, как же они применяются к реальному миру. Когда вы смотрите вокруг, вы видите перспективу с одной или двумя точками схода? Если горизонт всегда на уровне глаз, что случится, если вы посмотрите вниз? Что такое точка схода на самом деле? И можно ли вам забыть о перспективе, если вы не рисуете что-то связанное с архитектурой?
В этой статье я не объясню все правила модификации объекта в линейной перспективе. Существует множество уроков об этом, и при желании вы можете их найти самостоятельно. Вместо этого, я объясню вам, откуда взялись эти правила, и почему кому-то нужно было их изобрести. Правила, в конце концов, являются лишь одним способом описания удивительного феномена, существующего в природе с того самого дня, как наш мозг начал обрабатывать сигналы, полученные от наших глаз. После прочтения этой статьи вы больше не будете прежними!
Перспектива…И Что Такого?
Забудьте о математике и геометрии. Оглянитесь назад и вспомните те дни, когда вы путешествовали и наблюдали, как дома и объекты движутся вместе с вами. Ближайшие к вам объекты двигались быстрее всего, а объекты вдалеке едва ли меняли свое местоположение. И самый далекий из них, луна, не двигался вовсе — она была, и все еще есть, и всегда будет вне зависимости от того, куда вы пойдете.
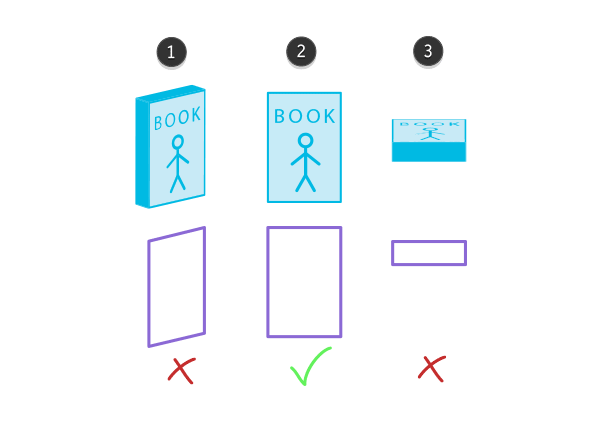
Мы склонны рассматривать 2 как истинную форму, в то время, как 1 и 3 лишь иллюзии, созданные перспективой
Но, конечно же, глупо было думать, что объекты двигались на самом деле, когда двигались вы. Это была просто иллюзия, подобная тому, что, например, ваш монитор или стол кажутся искаженными, если смотреть на них со стороны. Конечно, это прямоугольник, следовательно, это всего лишь иллюзия. Мы так привыкли видеть эти иллюзии, что больше не обращаем на них внимания, и, если ребенок спросит, почему двигаются здания, или почему так исказился стол, возможно, сначала мы даже и не поймем, о чем это он.
«Иллюзия» — это слово, которое мы используем, чтобы объяснить вещи, в которые наш мозг заставляет нас верить, хотя на самом деле они не реальны. Стол выглядит искаженным. Здание выглядит так, будто оно движется. Проблема в том, что все, что касается видения, есть иллюзия! Цвет, положение, длина, ширина, высота, поворот и даже текстура на самом деле не такие, какими их видим мы. Изображение в нашей голове есть лишь интерпретация реальности — интерпретация, неразрывно связанная с нами.
Размер
Насколько большой этот объект? Можете ли вы сказать?

Давайте добавим кое-что к этой сцене. Теперь это маленький квадрат, верно?
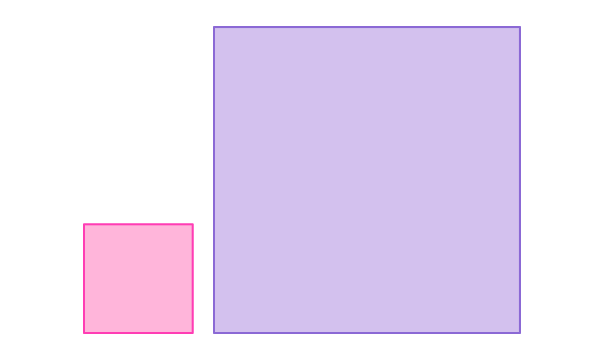
Или…может быть, он огромный.

Размер не существует сам по себе, а лишь по отношению к чему-либо. Ничто не является большим или маленьким само по себе — вам нужно сравнить это с чем-то, дабы определить размер. Обычно, мы используем «стандартный» размер чего-либо в качестве источника информации (большое яблоко — это яблоко, которое больше почти всех яблок, что вы видели в жизни).
Расположение
Но где наш квадрат? Он далеко или близко?

Теперь он выглядит далеким…

Но он также может быть и близко.
Он высоко?
Или, быть может, низко?
Объект не находится нигде до тех пор, пока вы не установили точку отсылки. Вам необходимо установить отношение между х и у, чтобы сказать, где находится х. Не интуитивно? Продолжайте читать. Я объясню все это позже.
Движение
Этот квадрат движется? Вроде бы нет, верно?
Постойте…мне это показалось?

Но…что же здесь движется на самом деле? Розовый квадрат, или призрак на заднем фоне? Мы никогда не узнаем! И даже если на первой картинке белый фон бы все время двигался, вы не заметили бы движения, пока что-то не изменилось бы на картинке.
Вы можете определить, движется ли что-то, сравнивая это с другим объектом, который не движется. Изменение расстояния между ними — это то, как вы измеряете скорость. Раньше люди считали, что Солнце вращается вокруг Земли, сейчас же мы считаем наоборот. Правда в том, что и первое и второе утверждение не правда — или же правда они оба.
В Чем Же Правда?
У всех этих примеров есть одна общая черта: чтобы они существовали, необходимо наличие отношения. Перспектива — это лишь название отношения между наблюдателем и другими объектами. Видите? Никакой математики.
Вы можете подумать: «Но ведь объекты просто находятся где-то, они не ждут, чтобы мы им сказали, что они там!» Это может выглядеть не интуитивно, но существует множество выражений, придуманных людьми, по отношению к нам:
- Если мне нужно значительно переместиться, чтобы достигнуть объект, он далеко.
- Если мои руки быстро устают, держа этот объект, он тяжелый.
- Если я едва чувствую объект в своей руке, он легкий.
- Если он жжется, когда я к нему прикасаюсь, объект горячий.
В зависимости от того, какое «я» вы используете, настоящий результат будет отличным. Для большинства людей он будет аналогичным, но вы можете быть силачом, и назвать холодильник «легким» — и вы не будете неправы! То, что мы называем «правдой», есть набор качеств, с которыми бы согласилось большинство людей. Холодильник тяжелый, потому что для большинства людей поднять его было бы проблематично — не потому, что он тяжелый сам по себе.
Что интересно, так это то, что выражения «далеко», «близко», «маленький», «тяжелый», «легкий» и т.д., меняют свое значение все время, в зависимости от переменных. Пульт далеко от вас, когда вам нужно встать, чтобы переключить канал (скажем, 3 метра), но в то же время, ресторан на следующей улице (300 метров) недалеко от вас.
Это может показаться вам философией, чем-то концептуальным, одним из многих способов описать реальность. Факт в том, что все эти вещи — размер, расположение, расстояние, движение — ни что иное, как концепция. Вообразите, что вы — некий бог, и вдруг вы можете видеть мир без этого вовсе! На самом деле, вы не можете этого представить — когда вы попробуете, вы, скорее всего, будете «летать, отделившись от тела», но все еще существуя, и наблюдая за всем с одной точки. Мы сами являемся своими точками отсылки, и это невозможно, как минимум для психически здорового, трезвого человека — вообразить вселенную без точки отсылки. Более того, «чувствовать», «трогать», «наблюдать» и другие выражения, подобные этим, подразумевают под собой рассматриваемый объект и того, кто рассматривает. Мы никаким образом не можем чувствовать объекты, не используя самих себя в качестве отсылки — до тех пор, пока мы люди, мы не можем знать, что что-либо представляет из себя в действительности. Математика может максимально приблизить нас к сути, но чем более точной она становится, тем меньше люди способны ее понять.
Каждое Чувство Имеет Свою Перспективу
Более точно, перспектива — это отношение между определенным чувством конкретного человека и предметом. Каждое чувство может иметь разные перспективы. Вот откуда появляются иллюзии — если изображение, полученное при использовании одного чувства, не совпадает с другими (или нашем знании о нем), мы говорим, что это неправда. Вы можете проверить это закрыв глаза в маленькой комнате с белыми стенами. Протяните ваши руки, и вы удивитесь, какой крошечной она стала!
Мы используем зрение, как наиболее важное чувство, поэтому мы склонны представлять, что реальность именно такая, как мы видим. Мир темноты, когда наши глаза закрыты, это другой мир, который мы предпочитаем называть неполноценным. Факт в том, что то, что мы видим, тоже неполноценно — наши глаза и мозг обрабатывают лишь малую часть всех существующих зрительных сигналов. Мы живем в реальности, которая существует только для нас, и похожа — но не обязательно идентична — для всех людей. Мы не знаем, как выглядит мир. Он воспроизводится прямо перед вашими глазами с каждым движением вашей головы. Поэтому объекты вокруг вас меняют свою форму, когда вы двигаетесь — это не иллюзия, они действительно меняются. Фигуры и формы существуют лишь у вас в голове, в качестве интерпретации определенной информации, обрабатываемой вашим мозгом. Нет «истинной» формы, той, что не создана вашим мозгом. Все они — прямые и искаженные — одинаковы. Зовите их всех иллюзиями, или же истинными формами.

Мы все получаем одинаковую информацию от объекта, но именно то, как она обрабатывается, создает изображение в нашей голове.
Так какое же отношение это все имеет к искусству? И где же перспектива, та перспектива, с идеально прямыми линиями и точками схода во всем этом?
Перспектива Создает Изображение
Я надеюсь, что не слишком вам наскучила своими длинными разъяснениями, ибо считаю, что это совершенно необходимо для того, чтобы действительно понять те вещи, о которых я буду говорить далее. Как художник, вы будете создавать оптическую иллюзию — вы используете линии и особые пигменты, чтобы заставить людей верить в то, что они смотрят на что-то, что они видели в реальности. Чтобы создать эту иллюзию, нужно учесть абсолютно все зрительные механизмы, известные нам. Вы не можете нарисовать тарелку с яблоками, потому что, как мы выяснили, мы не имеем понятия, что это такое. Вы рисуете увиденную вами тарелку с яблоками — тарелку, увиденную чьими-то глазами.
Вот тут-то все и начинается. Когда вы срисовываете с фото, или, пускай, с реальности, вы попросту копируете изображение, которое вы видите в своей голове. Вот почему достичь удивительных результатов в этом деле относительно просто — вам лишь нужны хорошие технические навыки и координацию руки и глаз; и первому и второму научиться просто.
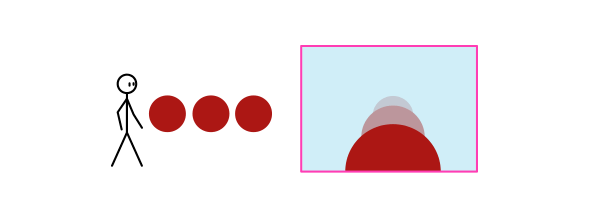
Большинство людей рассматривают сей процесс как «копирование реальности». Повторюсь: невозможно создать копию тарелки с яблоками при помощи кисти (А). Вы способны создать только визуальную копию (3) изображения в вашей голове (2), которое появляется, когда вы смотрите на тарелку с яблоками (1).
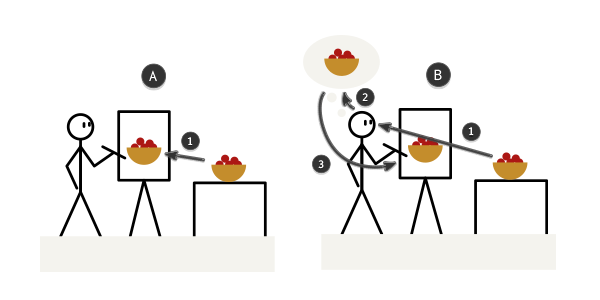
Мы приближаемся к действительному значению перспективы. Позиция наблюдателя, расстояние между его глазами и предметом, состояние его зрения — все это создает увиденное изображение. Отсюда следуют два важных вывода:
- Изображение объекта есть интерпретация мозга человека.
- Тот же самый мозг создаст бесчисленное количество различных изображений одного и того же объекта, когда изменится положение глаз.
А теперь, к сути. Когда вы смотрите на картину, вы видите не изображенный на ней предмет (А) — вы видите изображение, которое бы создал ваш мозг, если бы вы смотрели на предмет с одной четкой позиции, угла, в определенном свете и состоянии сознания (В).
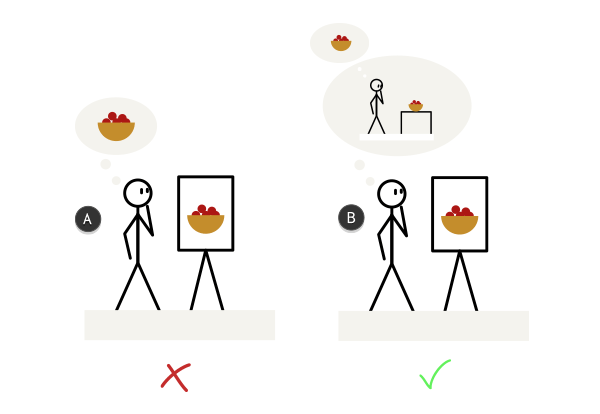
Если вы запутались, взгляните на иллюстрацию ниже. Когда вы смотрите на картину, вы представляете себя в качестве наблюдателя. В вашей голове вы воссоздаете условия и положение, а затем вы можете представить предмет в целом.
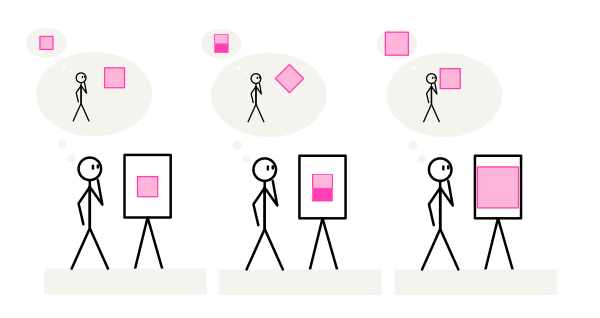
Набор параметров наблюдателя (позиция, угол и зрительный диапазон и т.д.) по отношению к среде — это и есть значение перспективы, которое мы используем, как художники.
Как Перспектива Влияет на то, Как Выглядит Предмет?
Все еще достаточно запутанно, не правда ли? Давайте еще немного узнаем о глубине.
Как же это возможно — увидеть 3D-изображение в 2D-картине? Так же, как и вы можете видеть глубину только одним глазом! На самом деле, бинокулярное зрение наиболее полезно в очень маленьком диапазоне — вы можете использовать его, чтобы вставить нитку в иголку или выполнять другие упражнения, требующие точности. В остальных случаях, как, например, определение «близко» и «далеко», мы используем наши наблюдения из прошлого. Мы знаем, насколько велико яблоко, когда мы держим его в своей руке, поэтому, если оно выглядит намного меньше, чем в первом случае, оно, должно быть, находится далеко. Для полной картины мы используем аккомодацию глаз, сравнение, свет и тень.
У наблюдателя есть только один глаз, до тех пор, пока у нас не появятся простые и доступные технологии для рисования 3D-картин. Но это, на самом деле, не важно! Когда вы видите 3D-модель у себя на экране, это 2D. Иллюзия глубины создается тогда, когда вы начинаете ее вращать. Тот же самый трюк используется и тогда, когда у вас один глаз — вы двигаете вашу голову, дабы изменить перспективу, и внезапно появляется глубина. Почему? Потому что у 2D изображений существует только одна перспектива. Если вы можете легко переключиться как минимум между двумя из них в каком-то общем измерении, она становится трехмерной для вашего сознания. Это происходит потому, что 2D сцена/объект может двигаться только вверх-вниз, влево-вправо или по диагонали. Когда он двигается в каком-либо другом направлении — к вам или от вас — добавляется третье измерение. Это третье измерение — глубина.

Но почему некоторые рисунки выглядят так, будто они трехмерные, когда у них существует только одна перспектива? Это потому, что некоторые перспективы подразумевают наличие других перспектив. Вы смотрите на них, и вашему мозгу достаточно легко представить, что бы случилось, если бы наблюдатель переместился. Другие изображения не дают никаких подсказок о наличии дополнительных перспектив, поэтому мы не сможем представить их верно. Если вам когда-либо было интересно, почему так легко нарисовать одна сторону персонажа, и так сложно сделать ее более динамичной, то вот ответ:
Существуют перспективы, которые передают лишь два измерения. Давайте называть их 2D перспективами. Так как лист бумаги тоже двухмерен (как минимум, с нашей точки зрения…), передать два измерения на нем вполне просто. Однако, вы не можете перехитрить третье измерение и ждать, что оно будет легко прочитываться! Рисование 2D перспективы неизбежно ведет к плоскому изображению — к чему-то, что, возможно, имеет третье измерение, но мы ничего не знаем об этом и предполагаем, что изображение его не имеет.
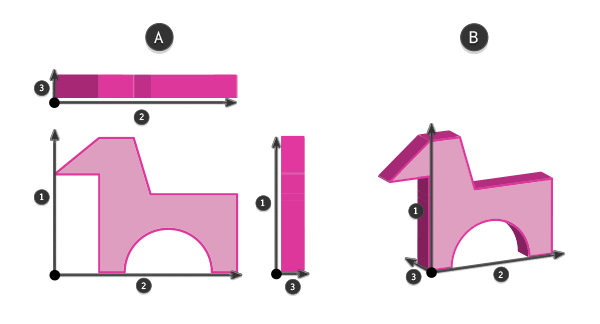
А — все изображения передают только два измерения, игнорируя третье. Поэтому, каждое из них выглядит плоским; В — изображение передает все три измерения, и, следовательно, выглядит трехмерным
2D перспектива, как я ее называю, известна в черчении, как ортогональные проекции. Рисуя как минимум две стороны объекта, мы можем определить, как он будет выглядеть в 3D. Однако, ни одна из проекций не является перспективой по умолчанию, потому что перспективы по умолчанию просто не существует. Повторюсь, будучи людьми, мы не обладаем чувством, которое бы позволило нам обрабатывать целый объект. Для нас, каждый объект состоит из бесконечных перспектив — и мы можем видеть только одну единовременно.

Ни одна из этих перспектив не является перспективой по умолчанию или истинной перспективой. Нет, даже этот «квадрат».
Итак, вот в чем проблема: вы не можете нарисовать что-либо без какой-либо перспективы. Это было бы сродни попыткам нарисовать предмет, который не видит никто! Следовательно, каждый раз, когда вы рисуете что-либо, вы передаете некоторую перспективу — не важно, знаете ли вы, делаете ли вы это или нет. К сожалению, когда вы пытаетесь учить что-то о перспективе, вы сталкиваетесь с техническим подходом с кучей странных, жестких правил. Вот так нужно рисовать горизонт, вот точка схода, одна, другая, третья, правильные углы, стены, повторяющиеся формы, порядок…Вы смотрите на них, вы их учите, но вы не видите никакого отношения к тому, что вы рисуете ради удовольствия. В конце концов, вы решаете, что все эти правила к вашему хобби не имеют никакого отношения, и игнорируете их.
И я через это прошла. Но давайте повторим еще раз: изображение создается, когда его видят. Когда вы видите что-то, перспектива создается автоматически. Следовательно, перспектива вшита во все, что вы рисуете. Вы можете учить ее или не учить — но избежать ее не выйдет.
Не вешайте нос! К счастью, научиться перспективе не сложно. В конце концов, вы делали это интуитивно годами! Вам просто нужно систематизировать ваши знания, и тогда вам больше не нужно будет угадывать. Перспектива для вас будет работать!

Это эффект принятия одной определенной перспективы за «истинную форму» объекта
Как Работает Перспектива?
Наконец, та часть, которую вы так долго ждали! Мы уже убедились в том, что перспектива — есть жизненно важная часть каждого рисунка, и не только технического. Но откуда она берется? Как создается единичная перспектива? Как и когда 2D перспектива превращается в 3D? И почему 3D-объекты в 2D изображении выглядят искаженными?
Откройте свое создание — это то, о чем вы, возможно, никогда раньше не задумывались. Это будет не интуитивно, потому что всю свою жизнь вы пользовались Евклидовой геометрией, и, как мы скоро узнаем, зрение работает совсем не так. Не просто перескочить с одного способа мышления на другой после всех этих лет, но это точно стоит того!
Три измерения
Давайте начнем с объяснения трех измерений. Возможно, вы знаете, что 2D — плоское, а 3D…ну, 3D, но как это работает? В чем разница между двух и трехмерными объектами?
Давайте начнем с, возможно, шокирующего факта — объекты на деле не 2D, 3D или 5D — они лишь погружены в измерения и воспринимаются нами, как целое изображение, сделанное из частей из каждого измерения. Поэтому куб может быть квадратом, квадрат может быть линией, и линия может быть точкой. Мы называем объект трехмерным, если он существует в третьем измерении в виде чего-то большего, чем точка.
Два измерения
Не важно, что мы называем измерениями. Что важно — так это то, что их три. Давайте начнем с двух.
Это 2D-лист, верно? Мы точно это знаем. У него есть длина и ширина, и это все, что нам нужно, чтобы нарисовать что-то плоское.
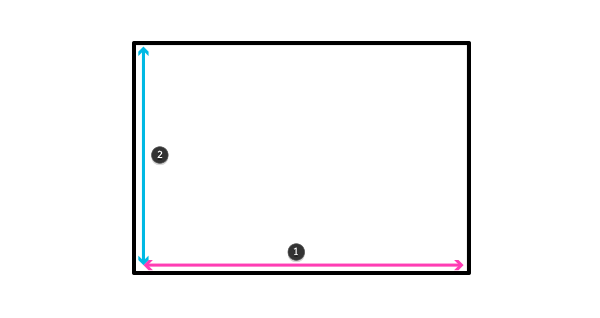
На самом деле, нет. Два индивидуальных измерения не дают нам ничего до тех пор, пока они раздельны. Линия имеет полную длину в двух измерениях только тогда, когда она им параллельна. В других случаях она короче, и когда она перпендикулярна, она становится точкой! Не упоминая уже о том, что линии, лежащие в перпендикулярном ряду, становятся одной.
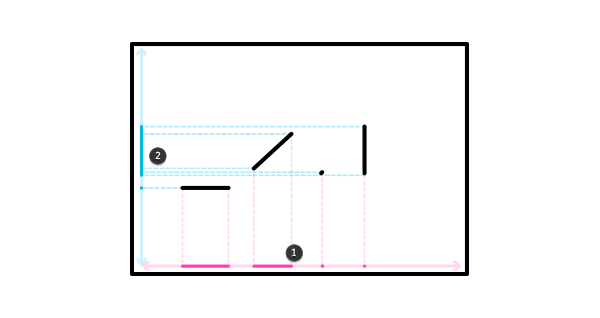

С точки зрения отдельных измерений, все эти линии совершенно разные
Чтобы создать реальное 2D-пространство, нам необходимо добавить второе измерение к каждой точке первого измерения…
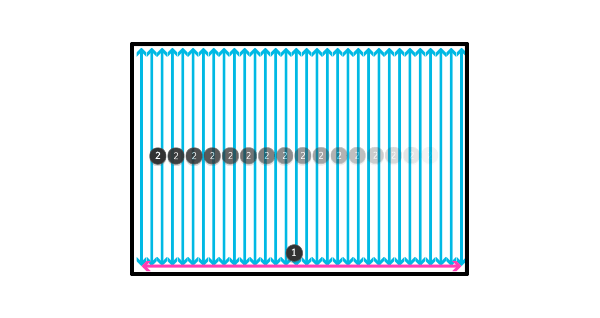
…и первое измерение к каждой точке второго измерения.
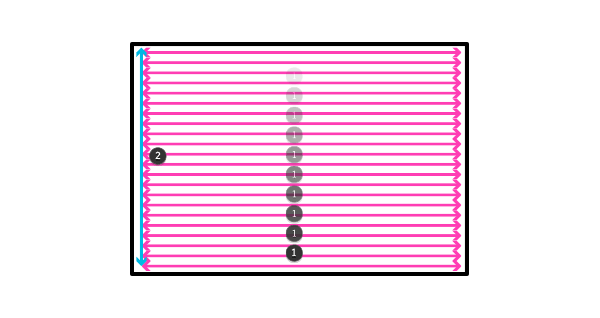
Может выглядеть запутанно, но мы создали пространство, которое разделяют два измерения. Сейчас, вне зависимости от того, куда пойдет линия, она будет зафиксирована обоими измерениями. Мы можем определить длину линии, даже если она не параллельна ни одному из измерений!
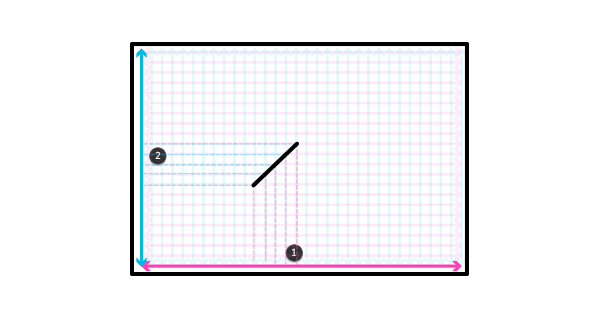
Например, когда линия не параллельна ни одному из измерений, финальное изображение создается при помощи объединения частей информации из каждого измерения, которое она пересекла.

Мистическое Третье Измерение
В 2D-пространстве мы можем переместиться влево, вправо, вверх, вниз, и везде между этими направлениями. Однако, нет таких понятий, как «вперед» и «назад», здесь нет «близко» и «далеко». Расстояние будет нашим третьим измерением — когда вы двигаете один 2D-лист под или над другим, создается глубина.
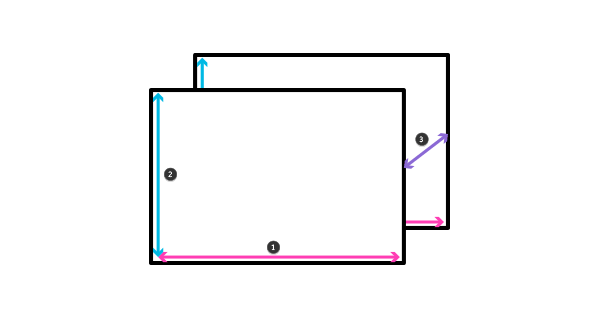
Чтобы создать 2D-пространство, для каждой точки одного пространства мы добавляли другое. То же самое и с 3D-пространством — для каждой точки третьего измерения нам необходимо добавить часть 2D-пространства.
Однако, и лист, и ваш экран — оба они 2D. Мы не можем представить здесь третье измерение! Иллюстрация ниже — лишь концепция, а не отражение реальности.
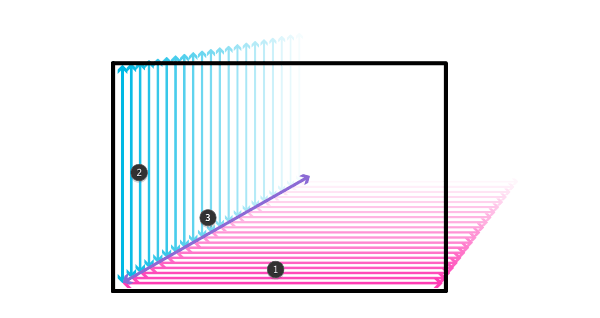
Если мы хотим нарисовать линию точно так, как она выглядит в одном измерении — нет проблем. То же самое с двумя измерениями. Но на этом все — мы можем нарисовать только два измерения одновременно на 2D-листе. Когда мы хотим добавить третье, оно сожмется в 2D-пространство — линии будут искажены, точно так же, как когда мы хотели нарисовать 2D-линию в одном измерении.
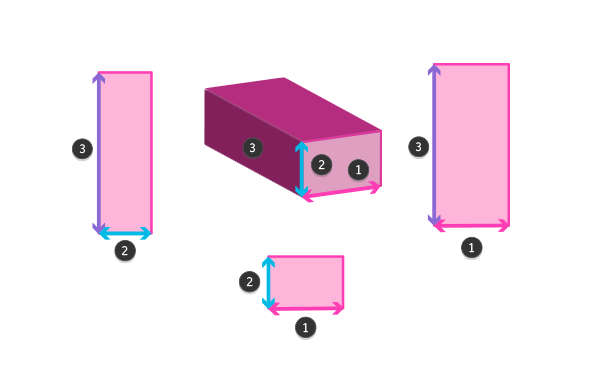
Мы можем изобразить только два неискаженных измерения в 2D-пространстве
Также важно заметить, что нет какой-то определенной стороны объекта, которая является «третьим измерением». Сейчас, когда вы можете легко переключаться между двумя измерениями, при помощи простого вращения, передняя часть может стать задней, а верх может стать низом. Все измерения отмечают объект, но он не является их частью.
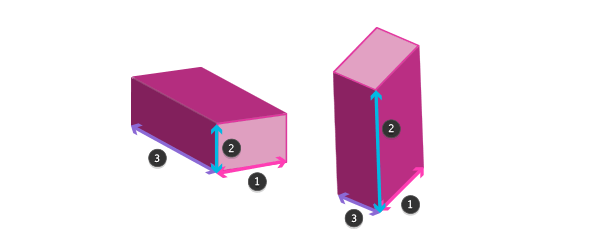
Интересный факт — мы могли бы добавить больше измерений — одно 3D-пространство для каждой точки четвертого измерения и так далее. В математике это очень просто, но мы, люди, воспринимаем только три измерения, и почти невозможно представить какие-то другие. Для нас это хорошо — в рисовании три измерения достаточно сложно понять!
Человеческое Поле Зрения (ПЗ)
К сожалению, из всего животного мира, наши глаза устроены не самым лучшим образом; на деле, даже, достаточно плохо. Хотя поле зрения обоих глаз составляет примерно 120 градусов, только в зоне 1 мы видим четкие детали и цвета. В зоне 2, все, что от этого остается, это цвета и размытые формы, а зона 3 используется, в основном, только чтобы видеть движение. Однако, наш мозг заполняет эти пробелы, и нам кажется, что изображение в нашей голове так же хорошо, как фото — с яркими, четкими деталями в любой его части. Он также убеждает нас, что нет этого размытого двойного носа прямо по центру нашего поля зрения.
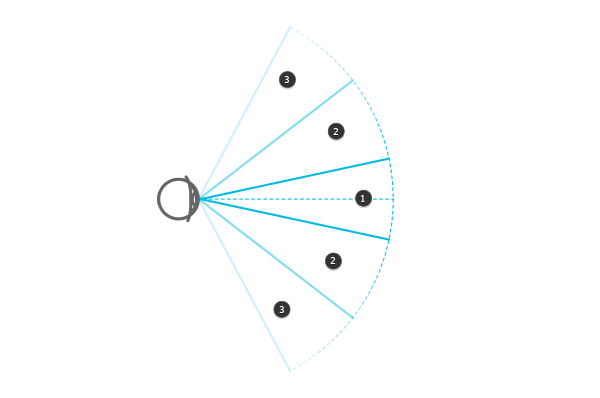
Конус нашего поля зрения образован бесконечным количеством 2D (горизонтальных и вертикальных) плоскостей, размещенных вдоль линии (расстояние — глубина) между глазом и бесконечностью. Для удобства, мы будем называть 2D-плоскости 2D-рамками. Второй конус — это то, как мы обычно это поле зрения представляем, но на деле он скорее похож на поле зрения камеры, чем человека.
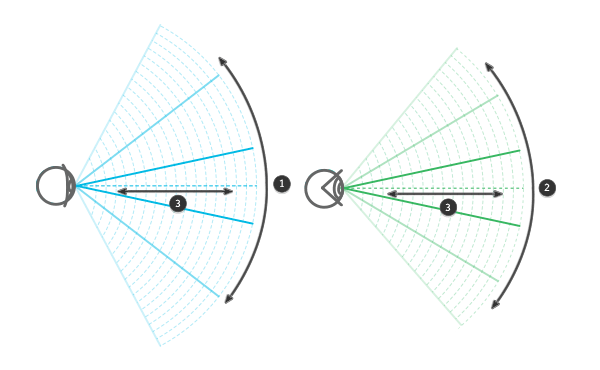
Иллюстрация четко показывает, как третье измерение связывает другие
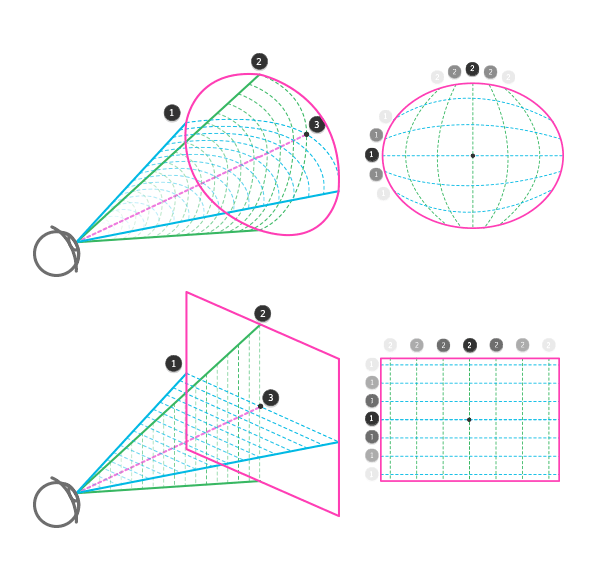
Первый конус — это то, что мы действительно видим. Второй — это то, что мы думаем мы видим
Верно — нет на деле «углов» зрения. Мы смотрим вокруг, а не вдоль вертикальных и горизонтальных линий.
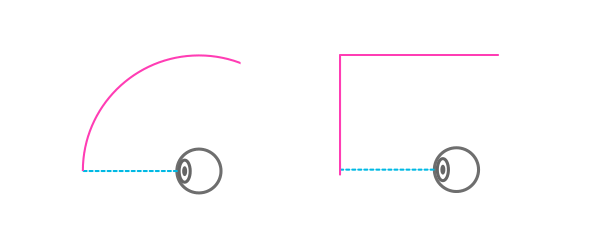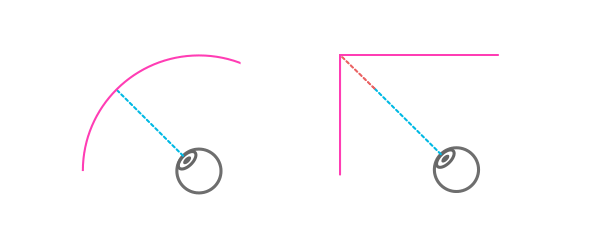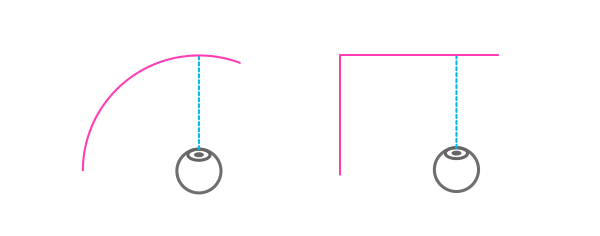
Тогда почему прямоугольник? Возможно потому, что это обычная фигура, которую легко воссоздать в виде холста или информационного массива. Это не имеет никакого отношения к нашему зрению, просто прямоугольник — фигура намного более практичная в использовании.
Представляю вам символическую интерпретацию ПЗ в простейшей конфигурации (использован только один глаз, более нам не нужно).
- Очки; использованы так, чтобы показать, где находится ваш глаз.
- Нос: он всегда находится там, но ваш мозг говорит вам, что это не так.
- Небо: в этой области все находится над вашей головой.
- Это область вашего роста.
- Земля: разместите объекты здесь, дабы они были устойчивы.
- Подземелье: если есть отверстие в земле или вместо земли — вода, вы можете использовать это пространство с пользой.
- Край вашего верхнего века.
- Край вашего нижнего века.
- Определенное расстояние между глазом и землей.
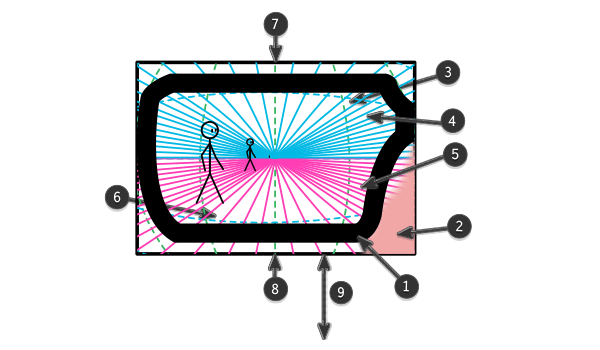
Важно помнить, где находится уровень земли. Если в качестве наблюдателя вы используете человека, представьте себе другого человека, ведущего диалог с наблюдателем прямо напротив него, с лицом, закрывающим большую часть рамки. Где бы они стояли? Именно на том месте и должна быть земля.
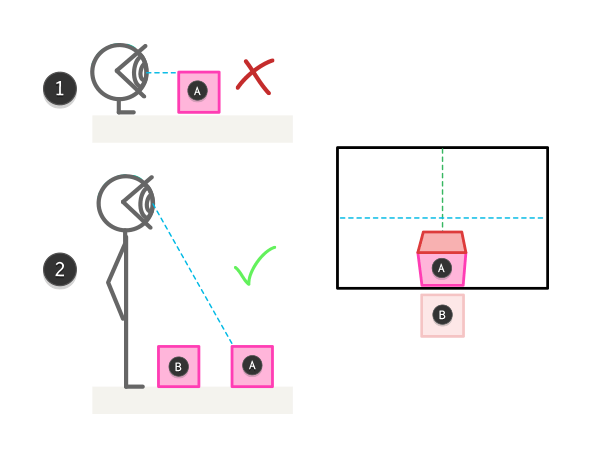
Вам не нужно использовать все ПЗ для вашей картины. Вы можете обрезать его, как вам хочется, поворачивать горизонт для создания чувства потерянного равновесия и размещать центр изображения вдали от середины. Экспериментируйте!
Шкала
Самую характерную черту перспективы — объекты, уменьшающиеся с расстоянием — можно легко объяснить при помощи конуса поля зрения.
В то время, как конус расширяется с увеличением расстояния, размер каждой рамки для нашего мозга не изменяется. Когда вы смотрите на что-то, расположенное очень близко к вам, вы не замечаете, что ваше поле зрения внезапно уменьшилось — вы видите лишь то, что объект увеличился по отношению к нему. С изменением расстояния объекты не изменяются, они попросту помещаются на разных рамках. Чем больше рамка, тем меньше кажется объект по отношению к ней. Поэтому вы можете накрыть весь мир своей ладонью — в определенной точке она действительно вполне может закрыть остаток конуса.
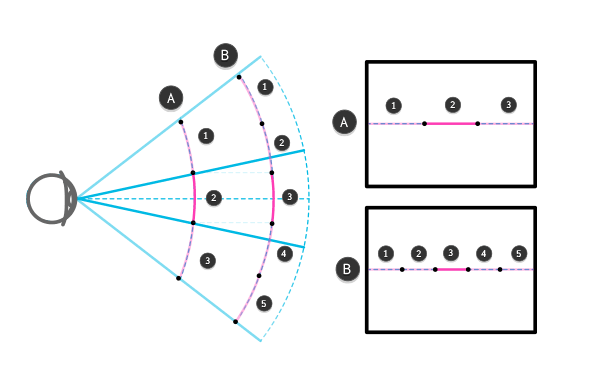
Три линии этого размера могут поместиться на рамке А, в то время как на рамке В таких объектов помещается пять. А и В одинаковой длины. Чтобы пять линий разместилось на рамке В, они должны выглядеть меньше, чем на рамке А.
Шкала также имеет отношение к воспринимаемой скорости объектов. Чем дальше объект, тем длиннее воспринятый путь между двумя сторонами. Просто сравните длину трех машин в ряду и дюжину больших зданий — и те, и другие вмещаются в линии с одинаковой длиной.
Это также объясняет, почему нам кажется, что задняя часть куба будто бы движется с иной скоростью, чем передняя — они расположены на разных рамках!
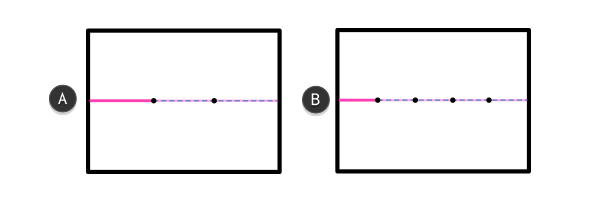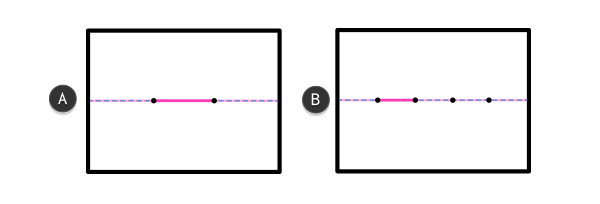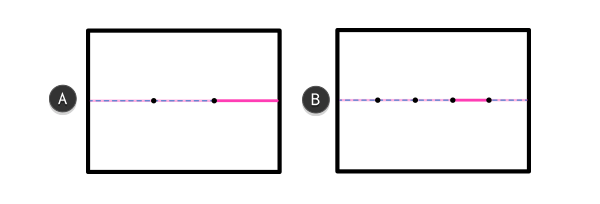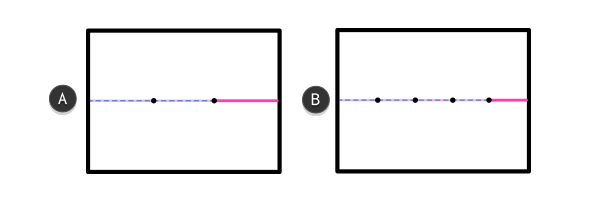
Линии на картинке В нужно больше времени, чтобы добраться до границы нашего зрения
Из-за того, что я только что описала, конечные изменения более всего бросаются в глаза в широчайшей части конуса. Яблоко, находящееся прямо перед вами, может заслонить весь мир, но с увеличением расстояния оно становится все менее и менее заметным. Поэтому в большинстве случаев мы игнорируем движение глазных яблок и предполагаем, что конус ПЗ начинается перед нашими головами — и вы можете свободно вращать глазными яблоками, не изменяя при этом положения головы — и перспектива не изменится.
Истинный размер
Теперь мы знаем, почему размер объекта меняется с расстоянием. Но как мы можем определить «истинный» размер? Когда же размер объекта выглядит таким, каким является в действительности? Если вы читали внимательно, вы должны знать ответ на этот вопрос — нет такого понятия, как «истинный размер». Когда вы измеряете что-то линейкой, вы сравниваете это с модульным размером в 1 сантиметр — модуль, который также меняется с расстоянием, и, следовательно, не является постоянным для ваших глаз. Невозможно измерить объект, изменяющийся в перспективе.
Однако, существует трюк, который наши глаза используют, дабы избежать неудобств. Первый ключ к определению размера — обратить внимание, насколько большую часть рамки он занимает.
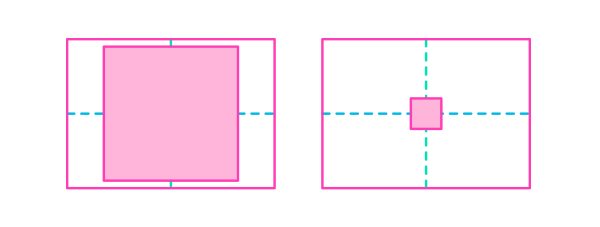
Мы уже отметили, что даже большие объекты уменьшаются с расстоянием. Как же мы, в таком случае, сможем отличить большой, но далеко расположенный объект от маленького, но расположенного близко? Нам нужен некий индикатор глубины, который и используют наши глаза, когда дистанция слишком велика, и бинокулярное зрение не несет никакой пользы.
Опыт
Это самое главное. Вы знаете, что здание достаточно большое, чтобы поместить вас внутри, следовательно, если для этого оно выглядит слишком маленьким, оно, должно быть, далеко.

Сравнение
Так как размер рамки постоянно изменяется, для приблизительного определения размера мы можем использовать пропорции. Это значит, что все внутри одной рамки будет уменьшаться в соответствии с каким-либо фактором, который вы можете использовать в своем уравнении, дабы вернуться к первичному результату. Поэтому мы зачастую используем человеческий силуэт во многих сценах — это сделано, чтобы подчеркнуть ее размер. Вы также можете использовать такие хорошо известные объекты, как деревья, горы (когда они кажутся маленькими по сравнению с главным объектом, он, должно быть, огромный), или траву (когда она огромная — главный объект, наверняка, крошечный).
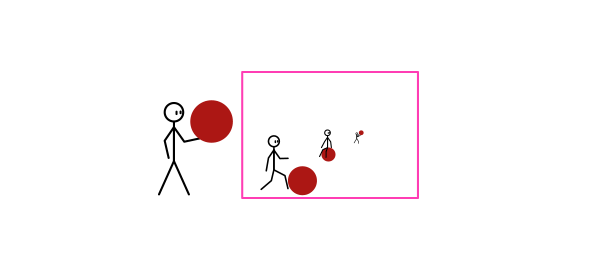
Глубина Поля (ГП)
Когда вы используете маленькую ГП, вы можете отделять близкие объекты от далеко расположенных. Легкий трюк, чтобы показать расстояние между наблюдателем и сценой — нарисовать какие-нибудь незначительные объекты перед наблюдателем и размыть их. Даже если вы не хотите использовать размытие, области, не расположенные в фокусе, должны быть менее детализированы.
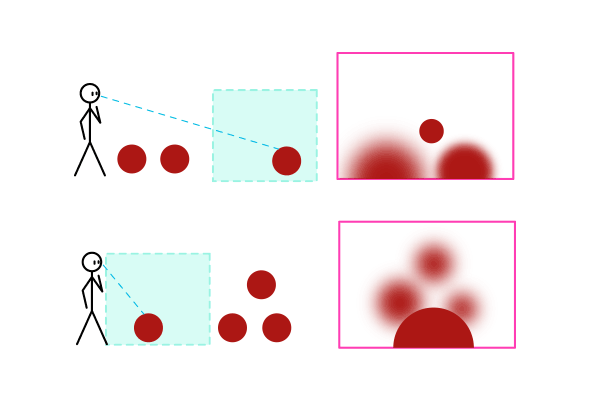
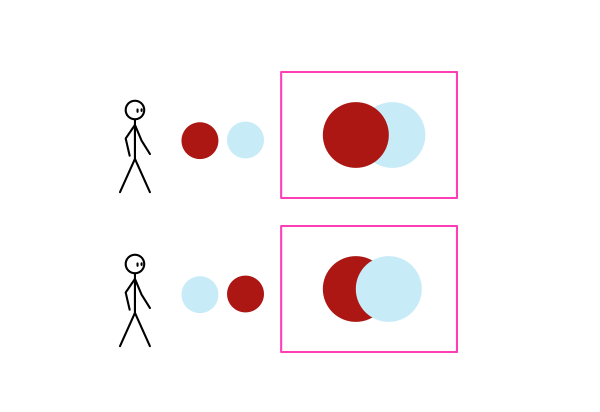
Перекрытие
Один объект может перекрывать второй только тогда, когда он расположен ближе, чем второй объект. Это многое говорит о расстоянии, а также это самый простой, интуитивный метод создания глубины.
Атмосферная Перспектива
Об этом вы можете прочесть в другой моей статье, но вот в чем суть: чем дальше что-либо находится, тем больше рассеивается цвет неба между вами и этим предметом. Когда воздух очень чистый, это не работает, но в большинстве случаев более размытый объект = дальше расположенный объект.
Комбинируя все эти трюки, вы сможете достичь той же глубины, что видят одноглазые люди. Также есть классный эксперимент для проверки того, насколько хорошо ваш мозг воссоздает глубину из 2D картинки. Найдите большее фото в хорошем качестве (фото на экране компьютера приемлемо), закройте один глаз и сделайте «телескоп» из вашей ладони. Посмотрите через него на фото, чтобы видеть только картинку и ничего больше. Существует хороший шанс того, что вы увидите ее в 3D!
Искажения
Если вы смотрели внимательно на наш конус, вы должны были заметить одну странную вещь. 2D плоскости на самом деле не плоские — они выглядят, как неглубокие тарелки. Это значит, что они сферические, как Земля, и также, как мы не можем создать идеальную, неискаженную 2D карту, мы не можем создать 2D рамку без искажения.
Иллюстрация ниже четко показывает, что линия, хоть она и расположена перпендикулярно к линии зрения, касается двух разных рамок. Как мы знаем, чем дальше рамка, тем меньше объект — так что часть линии станет меньше, делая всю линию короче и повернутой от нас!
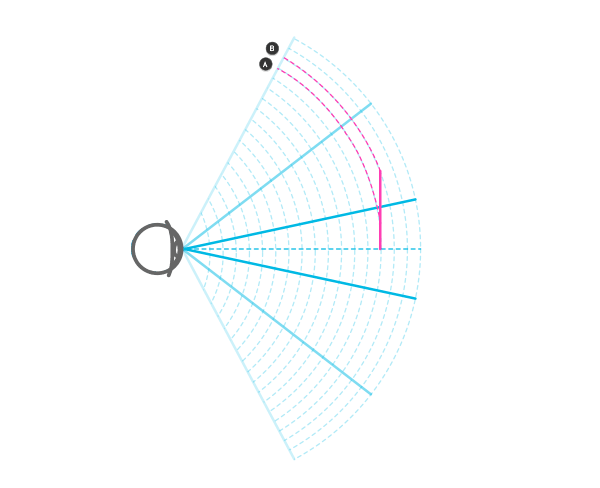
Чтобы получить вероятно неискаженное изображение, объект должен быть помещен прямо в центре конуса ПЗ так, чтобы все его стороны были перпендикулярны линии зрения. В случае 3D объектов это невозможно — поэтому они всегда выглядят искаженными.
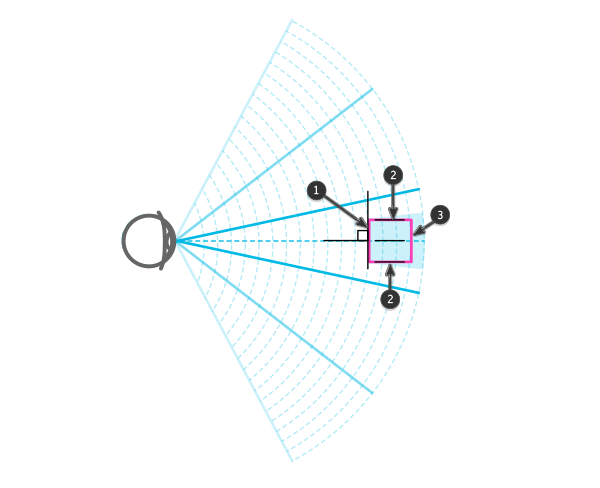
1 — линия перпендикулярна линии зрения, поэтому она воспринимается, как прямая и с полной длиной; 2 — линии параллельны линии зрения, поэтому они выглядят, как точки; 3 — линия лежит в «тени» первой линии, поэтому ее мы не увидим вообще
Кстати говоря, объектив камеры также улавливает искажение, но оно обычно нежелательно, и обрезается сенсором. Широкоугольные объективы принимают часть искажения, в то время как объектив фиш-ай принимает его полностью. На самом деле, наши глаза работают, как фиш-ай объектив, а наш мозг говорит нам, что мы видим прямые линии! Не верите? Скоро я объясню это подробнее.
Давайте разберемся, как это работает. Когда мы хотим увидеть другую сторону куба, нам нужно его повернуть. Однако, в то же время, перпендикулярность первой стороны теряется — обе стороны располагаются вдоль нескольких рамок на разном расстоянии (глубина). Поэтому, некоторые их части выглядят дальше расположенными и более короткими — то есть, повернутыми.
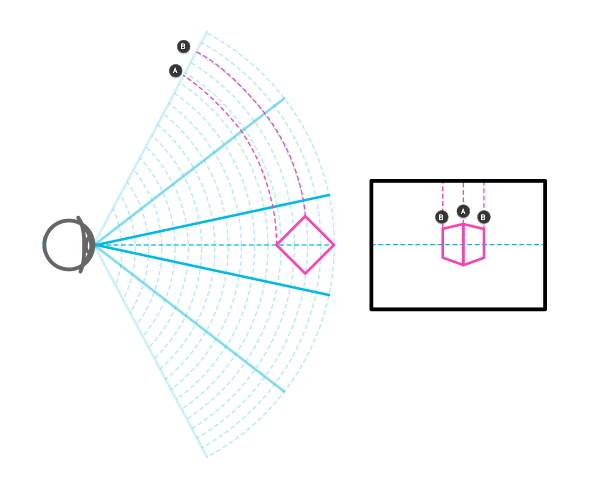
Вот так решается первая загадка. Но есть ли какой-либо способ предвидеть искажение без того, чтобы сначала рисовать 2D-вид со всеми кривыми?
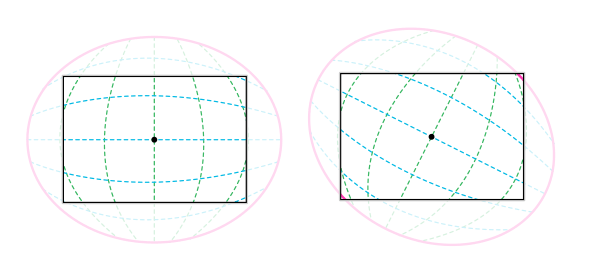
Для начала вам необходимо помнить, что у нас есть два горизонта — горизонтальный и вертикальный. Нам так знаком горизонтальный горизонт, что мы даже не замечаем второй. Но, конечно же, это не значит, что он не существует!
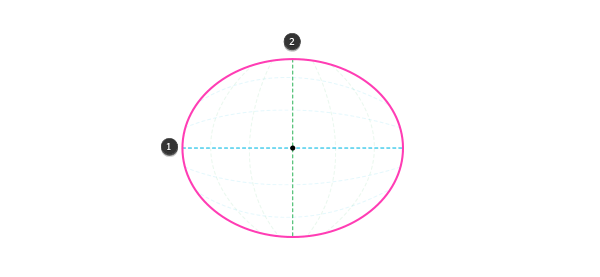
1 — горизонтальный горизонт; 2 — вертикальный горизонт
Оба горизонта пересекаются прямо в центре, в точке, на которую вы смотрите. Вы можете перемещаться вдоль горизонта, вверх и вниз, что, по факту, то же самое, что и перемещение влево и вправо. Пока давайте предположим, что лево и право относятся к горизонтальному горизонту, а верх и низ относятся к вертикальному.
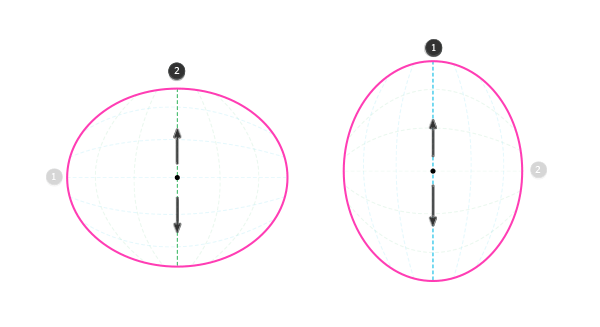
Вы также можете двигаться крест-накрест, например, вверх по одному горизонту и влево по другому.
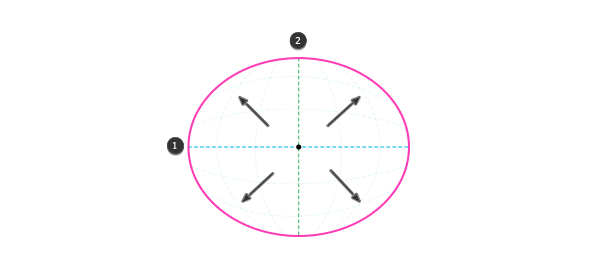
Центральная область выглядит ближайшей к нам. Это также и наименее искаженная область. Поэтому она используется как полный кадр и основа для линейной перспективы. Однако, этот подход не объясняет, почему линии гнутся!
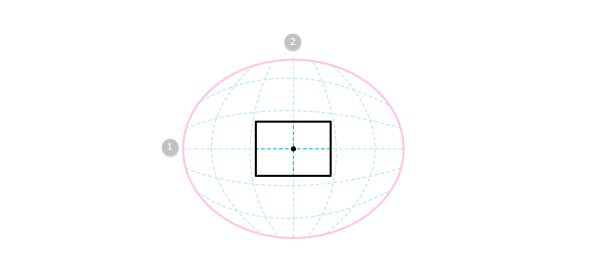
Помните, что изображение в вашей голове — сферическое; лишь ваш мозг сообщает вам, что оно абсолютно прямое. Когда вы фокусируетесь на небольшой области в центре (А), закругление линий не так заметно, но в большем масштабе это критично для построения верного 3D изображения. Внимательно взгляните на иллюстрацию ниже.
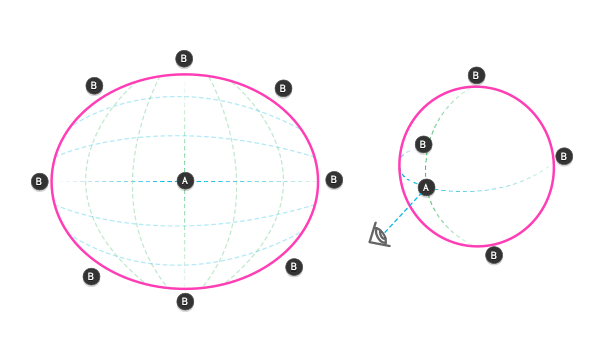
Представьте ряд кубиков, стоящих вдоль горизонта, параллельно вашим глазам. Тот, который находится в точке А будет казаться вам ближайшим, в то время как другие будут казаться удаляющимися.
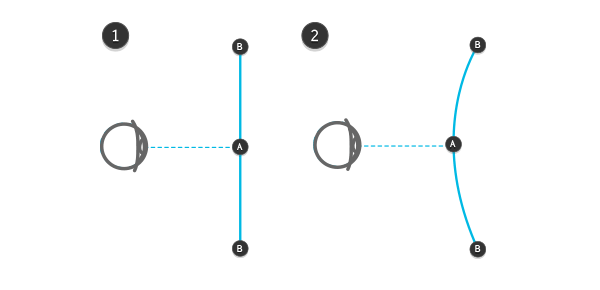
1 — «истинная» линия; 2 — наблюдаемая линия
Почему? Это то же искажение, о котором мы говорили ранее. Теперь давайте поговорим о передних гранях этих кубиков. Обе точки А лежат на одной рамке, поэтому они воспринимаются с одинакового расстояния, однако, между точками B и C существует разница в глубине. Для точек E и D эта разница огромна!
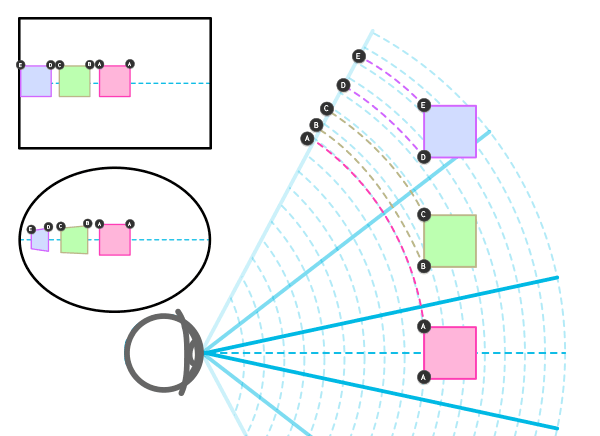
Если вам все еще неясно, как возможно то, что мы получаем выпуклое изображение на вогнутой рамке конуса, вот ответ:
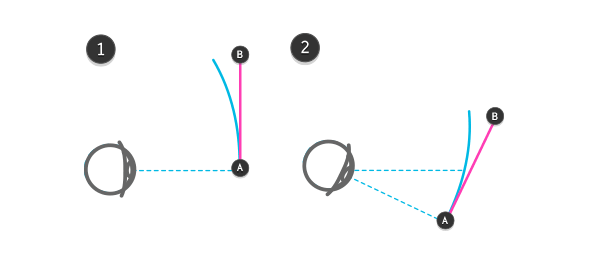
Когда вы вращаете вид, становится очевидно, что точка B расположена дальше от нас, чем А
Основное заключение всего этого — это иллюстрация ниже. Лучший и простейший урок, который вы можете получить о перспективе, это:
Чем выше объект над* горизонтом, тем больше его нижней** и меньше его передней части видно нам
Теперь вы можете создать по этому примеру аналогичные ситуации, с «*ниже» и «**верхней части», или с «*левее» и «**правой части» и так далее. Просто создавайте пары из противоположных сторон и правило будет работать! Дополнение к этому уроку:
Чем дальше линия от центра, тем она короче
Это, пожалуй, все. Что? Слишком просто? Где точки схода и все такое…? Если вы действительно хотите знать, то вот ответ:
Недостатки Линейной Перспективы
Линейная перспектива есть упрощенная версия того, о чем мы с вами говорили. Давайте разберемся, как такое возможно.
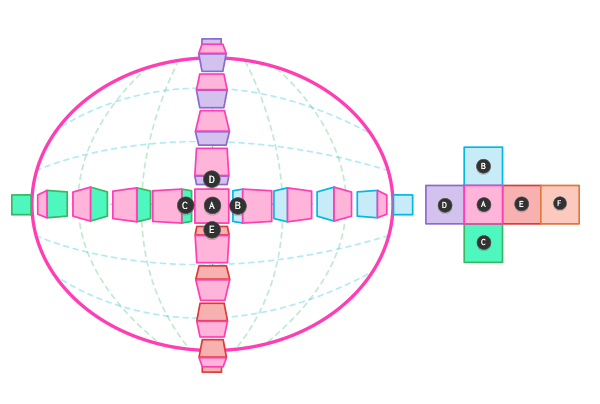
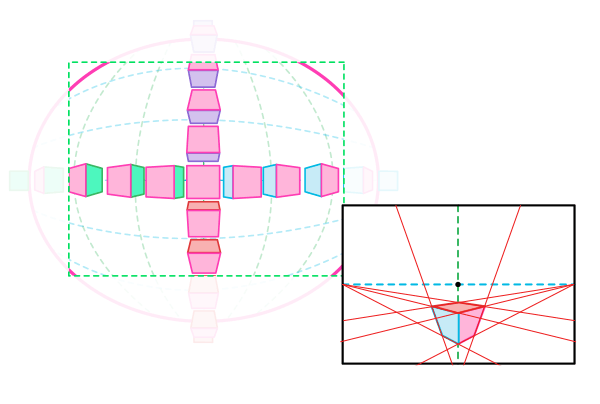
Перспектива 0-ой Точки
В этой перспективе все прямые линии параллельны или перпендикулярны друг другу. Они не сходятся ни в какой точке. Мы можем наблюдать такую перспективу, глядя в центр нашего ПЗ, когда объект стоит прямо перед нами.
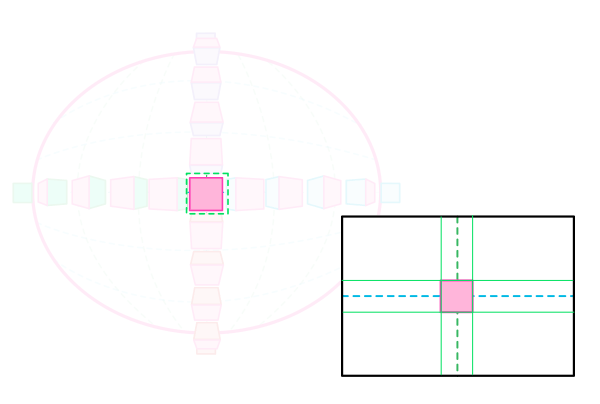
Перспектива с 1 Точкой Схода
В этой перспективе все линии, которые не параллельны или перпендикулярны друг другу сходятся в одной точке на горизонте. Этот эффект идентичен тому, который наблюдается в центральной области, кроме того, что в реальности появится искажение. Для этого объектам необходимо стоять перпендикулярно линии зрения.
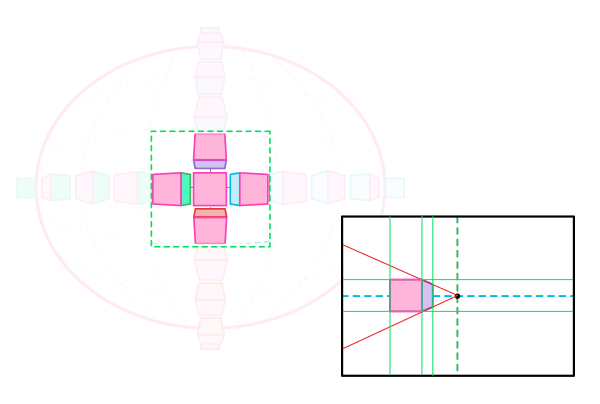
Перспектива с 2 Точками Схода
В этой перспективе существует 2 точки на горизонте, где сходятся все линии, кроме тех, что параллельны друг другу. Мы можем наблюдать этот эффект расширив центральную область. Здесь объекты могут быть повернуты.
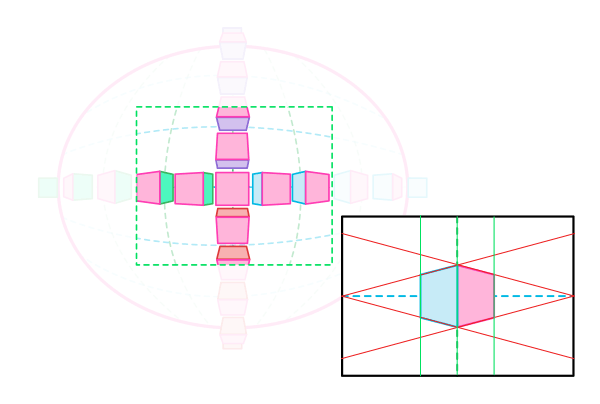
Перспектива с 3 Точками Схода
В этой перспективе нет параллельных или перпендикулярных линий. Они все сходятся в одну из двух точек на горизонте, или в третью точку на вертикальном горизонте. Этот эффект можно наблюдать периферийно, особенно верх/низ (например, смотря на высокое здание). Вращение приветствуется.
Почему Так Сложно Ей Пользоваться?
Существует две основные причины, по которым линейная перспектива выглядит столь неинтуитивно и удерживает вас от спонтанных рисунков.
Во-первых, точки схода относятся не к позиции наблюдателя, но к объектам по отношению к ним. Каждый объект имеет свои собственные точки схода, поэтому проще всего расположить их все в ряд таким образом, что они все будут иметь одинаковые точки схода. Если вы приготовите одну сетку перспективы и отдадите ей все объекты, вы получите жесткое, сделанное человеком пространство — и потеряете контроль над композицией. С другой стороны, чем больше точек схода, тем больше хаоса и работы для вас.
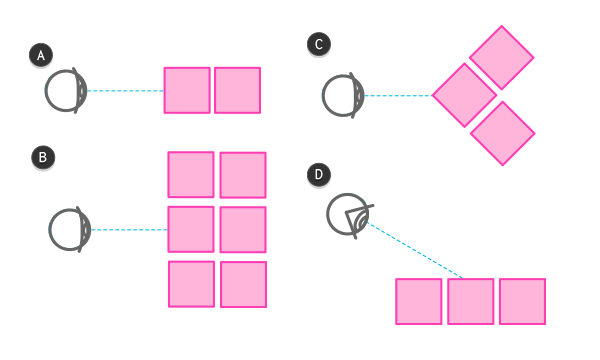
А-0 ТС; В-1 ТС; С — 2 ТС; D — 3 ТС
Во-вторых, только объекты, созданные человеком, имеют тенденцию быть достаточно правильными, чтобы располагать на них линии. Органические вещи, такие, как живые существа, подчиняются правилам перспективы, как и все остальное, но они слишком динамичны, чтобы сковывать их жесткими линиями. Поэтому использование линейной перспективы для живых существ попросту убивает их дух. Как часто лев стоит прямо, с его сторонами, расположенными перпендикулярно к вам?
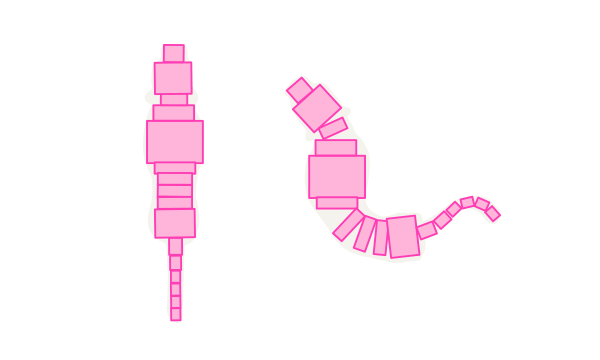
Представьте попытки использовать линейную перспективу на второй, более интересной форме!
Заключение
Перспектива — не самая легкая тема — ну а какая тема легка? Если вы хотите стать хорошим художником, невозможно избежать подобных вещей. Если тема для вас все еще непонятна — не переживайте, пусть ее понимание займет столько времени, сколько нужно; разделите ее на части и изучайте очень внимательно. Я твердо верю в то, что это база всего, что касается воссоздания реальности. Да, это сложно, но поверьте, после этого все будет легко!
Перспектива позволяет вам нарисовать мир, увиденный со спины лошади, или дракона, глазами маленького червячка или летящей птицы. Она создает динамику, движение, жизнь. Она превращает жесткую рамку в яркое воспоминание. Если вы хотите вдохнуть жизнь в свои рисунки, перестаньте думать только об изображаемых объектах, и сфокусируйте свое внимание также и на наблюдателе. Без них не было бы никакой картины!
Первое правило линейной перспективы — выучите ее, дабы у вас появилась возможность ее отбрасывать. Я надеюсь, что после этого урока вам не захочется что-либо отбрасывать — это знание, которое подарит вам творческую свободу в подчинении правилам видения. Применяйте линейную перспективу к зданиям и планам комнат, а также ко всему, где вам просто нужно разобраться, что происходит в вашем рисунке. Вы только что совершили огромный шаг навстречу превращению в великолепного художника!




